Time complexity and Big-O Notation

What is time complexity?

Wikipedia defines time complexity as

[…] the computational complexity that describes the amount of computer time it takes to run an algorithm.

Usually this describes the worst case scenario. You can also add best case and average case scenarios to get a more fine-grained comparison.

Why should I care about time complexity?

Time complexity calculations are irrelevant if your array contains a handful of elements. But it can make a huge difference with a large number of elements. It’s relevance increases exponentially.

As an example let’s say one operation takes 1ms. Here’s how the computation time explodes for an O(n * m) algorithm as compared to an O(n) algorithm:

1. objA.length und objB.length be 10:

O(n) = 10ms O(n * m) = 100ms

Difference: 10 fold

2. objA.length und objB.length be 1000:

O(n) = 1s O(n * m) = 1000s (over 16 minutes!)

Difference: 1000 fold

3. objA.length und objB.length be 10000:

O(n) = 10s O(n * m) = 100000s (over 27 hours!)

Difference: 10000 fold

Verdict: Time complexity is a very important topic for large arrays.

Example

This is an example of a very simple way to implement the following problem:

Add product’s (identified by _id) count values together from two lists.

Naive solution with 2 for loops

Complexity: O(n * m)

Actually it’s a bit mean to call something a naive solution, but it’s more of the mathematical sense here, meaning, a simple one. And simple might even have a positive connotation.

const objA = [
  { _id: 0, productName: "ProduktA", count: 15, discrition:"Test01"},
  { _id: 1, productName: "ProduktB", count: 31, discrition:"Test02" },
  { _id: 2, productName: "ProduktC", count: 43, discrition:"Test03" },
  { _id: 3, productName: "ProduktD", count: 1, discrition:"Test04" },
];

const objB = [
  { _id: 0, count: 3 },
  { _id: 1, count: 1 },
  { _id: 2, count: 4 },
  { _id: 3, count: 10 },
];

for (let i = 0; i < objA.length; i++) {
  for (let j = 0; j < objB.length; j++) {
    if (objA[i]._id === objB[j]._id) {
      const addition = objA[i].count + objB[j].count;
      console.log(addition);
    }
  }
}

Here the best case equals the worst case, because the loops will finish every time.

Functional solution: Hidden O(n^2) time complexity

Sometimes we are proud of elegant solutions but overlook time complexity issues.

Here an example which hoped to improve the solution, but it’s time complexity is as slow as the example above, i.e. O(n * m)

objA.forEach(
  item => item.count += objB.filter(
    itemB => itemB._id === item._id).length === 0 ?
    0 :
    objB.filter(itemB => itemB._id === item._id)[0].count
);

• Also, it’s a bit hard to read.

Functional solution 2:

Again, time complexity equals O(n * m)

const results: number[] = objA.map(itm => {
  return itm.count + objB.find(o => o._id === itm._id).count
})

• Oddly here its performance is much better than the for loop example:

  

• By using the find function here, the best case and average case here are faster than the worst case. That is because the find function will terminate it’s loop as soon as it finds a matching _id.

Fast solution

/**
 * Function which transforms an Array into an Object so that later access to the
 * fields of each entry in the array have a reduced complexity of O(1) instead of
 * O(n) because I don't need to loop through an array anymore but have direct access
 * to fields in an object.
 */
function normalize(arr) {
  return arr.reduce((agg, value) => {
    agg[value._id] = value;
    return agg;
  }, {});
}

// Here the objB array is made to an object. The transformation costs O(n).
const _objB = normalize(objB);

// Here I run through array A in time complexity 0(m) because accessing _objB
// only costs O(1) each time.
const computed = objA.map(value => {
  return { ...value, count: value.count + (_objB[value._id] ? _objB[value._id].count : 0) };
})

• The complexity calculation of this solution:

  O(n) + O(m * 1), i.e. O(m + n) which can be reduced to O(n) because m is a constant (fixed size).

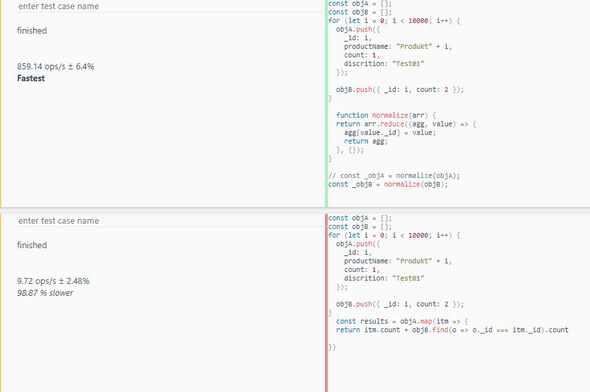
It’s performance is much better as compared to the other algorihms when testing performance with JSBench for long arrays: